How to use g2o #1 (nonlinear optimization library)

Abstract

g2o GitHub: https://github.com/RainerKuemmerle/g2o
테스트 환경: Ubuntu 18.04 with QtCreator
이번 포스트에서는 g2o 라는 optimimization library를 소개하고 예제를 통해 사용방법을 설명한다. 특히 이번 포스트에서는 optimizer의 다양한 옵션에 대해 알아본다. 다음 포스트에서는 graph의 다양한 vertex(node), edge 타입에 대해 설명한다.

1. Introduction to g2o

1.1 g2o 란 무엇?

GitHub을 보면 이렇게 소개되어 있다.

g2o - General Graph Optimization
g2o is an open-source C++ framework for optimizing graph-based nonlinear error functions. g2o has been designed to be easily extensible to a wide range of problems and a new problem typically can be specified in a few lines of code. The current implementation provides solutions to several variants of SLAM and BA.

한 줄 요약: C++ based nonlinear graph optimization library for SLAM and BA
풀이를 하자면 이렇다.

C++: 기본 언어는 C++이고 python 버전도 있는 듯 하다.
graph: 어떤 대상을 node와 edge로 추상화한 네트워크 형태의 구조물이다. node는 주로 구하고자 하는 객체의 상태 파라미터를 나타내고 edge는 node사이의 관계나 이를 측정한 데이터이다.
optimization: graph에서 node 파라미터와 edge 정보의 불일치를 계산한 것을 목적 함수(objective function)이라 하는데, 이 목적 함수를 최소화하는 node 파라미터를 계산하는 것이다.
nonlinear optimization: 목적 함수가 파라미터들의 weighted sum으로 나타낼 수 없는 nonlinear 함수여도 최적의 해(node 파라미터)를 구해줄 수 있다.
library: g2o를 빌드하면 최적화를 실행해주는 실행파일도 제공하고 C++ 프로젝트에서 그 기능을 활용할 수 있게 라이브러리 파일도 제공한다.
SLAM (Simultaneous Localization and Mapping): 주변 환경을 인식 할 수 있는 센서를 가진 이동체가 이동하면서 자신의 위치를 추적하고 동시에 주변 환경 지도까지 추정하는 기술이다.
BA (Bundle Adjustment): (주로 단안) 카메라로 optimization을 이용한 SLAM을 BA라 한다.

1.2 g2o말고 다른 건 없나?

nonlinear graph optimization을 해주는 라이브러리는 이것 말고도 GTSAM, MRPT 등 몇 가지 더 있는듯 하다. 다른 것들은 홈페이지도 잘 꾸며놨고 document도 잘 되어있다. 반면에 g2o는 딸랑 깃헙 README.md 가 전부이다. 사용법은 Example 들을 보며 추정해야 한~~다는게 실화~~다. 소프트웨어가 아직까지 잘 관리되고 있는지 보기 위해 세 라이브러리의 마지막 릴리즈 날짜를 보자.

g2o: 2017-07
gtsam: 2017-08
mrpt: 2018-04

세 라이브러리 모두 마지막 릴리즈는 좀 시간이 지났지만 꾸준히 자잘한 버그나 새로운 환경에 적응하기 위한 micro commit은 올라오고 있는 듯 하다.

그렇다면 성능은? 구글링을 해보면 g2o와 gtsam을 비교한 자료가 있긴 하다.

https://www.cnblogs.com/reinforce/p/5510539.html
http://www.wseas.us/e-library/conferences/2013/Paris/ECCS/ECCS-31.pdf

결론은 g2o로 최적화한 SLAM의 성능이 gtsam보다 살짝 더 정확하다. 살짝이긴 한데 1% 정확도 향상에 목메는 SLAMer 로서는 신경쓰이는 부분이다. 하지만 그 약간의 성능 때문이 document도 없는 불친절한 라이브러리를 설명하기 위해 이렇게 시간을 쓰고 있는 것은 아니다.
g2o를 쓰려는 이유는 SLAM의 정석(?)으로 불리는 ORB SLAM과 LSD SLAM에서 g2o가 사용되기 때문이다. 이 논문들의 소스 기반으로 혹은 일부 사용해서 발전시키는 연구를 한다면 평소에 g2o를 쓰는게 나을 것 같다.

1.3 포스트 작성 의도

이 포스트를 작성하는 이유는 방금도 말했지만 g2o는 공식적인 tutorial이 없다. 간단한 예제를 설명한 블로그들이 있긴 한데 다양한 용법을 보여주진 못 한다. ~~사실 영어라서 읽기 귀찮다.~~ 아니 무엇보다 GitHub star가 999개(998개 였는데 방금 내가 눌렀다. 곧 천개 될듯)나 되는 라이브러리에 이렇게 설명이 없다니 신기할 따름이다. 그래서 내가 공부하는 김에 다양한 용법을 정리하고자 이 포스트를 작성한다.

2. Install Guide

설치는 GitHub에 나온대로 간단하다.

2.1 Dependencies

GitHub에 나온 g2o의 dependency들을 설치하는 명령어는 다음과 같다.

sudo apt install cmake libeigen3-dev libsuitesparse-dev qtdeclarative5-dev qt5-qmake libqglviewer-dev

나는 Qt5를 qt archive에서 받아 설치했으므로 qt를 제외한 나머지만 설치하였다.

sudo apt install cmake libeigen3-dev libsuitesparse-dev

2.2 Build

빌드는 간단하다. clone 받고 cmake, make 하면 된다.

git clone https://github.com/RainerKuemmerle/g2o.git
cd g2o
mkdir build
cd build
cmake ../
make

3. How to use g2o with example

g2o를 사용하는 방법을 예제를 통해 설명한다. 단순히 예제 코드만 설명하는 것이 아니라 관련된 다른 사용법에 대해서도 언급할 것이다. 전체 예제 코드는 내 GitHub서 보길 바란다. 여기서는 코드를 잘라서 설명한다.

3.1 Include headers

#include "g2o/core/sparse_optimizer.h"
#include "g2o/core/block_solver.h"
#include "g2o/solvers/dense/linear_solver_dense.h"
// #include "g2o/solvers/csparse/linear_solver_csparse.h"
// #include "g2o/solvers/cholmod/linear_solver_cholmod.h"
#include "g2o/core/optimization_algorithm_levenberg.h"
// #include "g2o/core/optimization_algorithm_gauss_newton.h"
#include "g2o/core/factory.h"
#include "g2o/types/slam3d/vertex_se3.h"
#include "g2o/types/slam3d/edge_se3.h"
// #include "g2o/types/sba/types_six_dof_expmap.h"

// G2O_USE_TYPE_GROUP(slam2d);
// G2O_USE_TYPE_GROUP(slam3d);

헤더의 이름을 보면 대강의 기능을 알 수 가 있고 주석 처리된 줄들은 이 예제 외에 다른 문제를 풀 때 필요할 수 도 있는 헤더들을 참고사항으로 넣은 것이다.

g2o/solver/ 아래 헤더들은 선형식으로 근사화된 문제를 풀 수 있는 세 가지 알고리즘을 가지고 있는데 dense, csparse, cholmod 이다. 이 중 자신이 사용할 방법을 include 하면 된다. optimization_algorithm_xx.h도 마찬가지다. 선택사항에 대한 내용은 뒤에 설명한다.

g2o/types 아래에는 SLAM이나 BA에서 자주 사용되는 상태 표현들이 사용하기 쉽게 클래스로 정의되어 있다. 대표적으로 3차원 pose를 표현하는 SE3Quat 등이 있다. g2o는 2차원과 3차원의 자세와 좌표 등을 표현 할 수 있는 다양한 자료형을 제공한다.

G2O_USE_TYPE_GROUP(slam3d);는 그래프를 *.g2o 파일로부터 읽어올 때 필수적이다. g2o는 그래프 상태를 *.g2o 파일로 입출력 할 수 있는데 본 예제에서는 출력만 하므로 필요하진 않다.

3.2 Create an optimizer by 4 steps

// step 1. create linear solver
std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linear_solver = 
g2o::make_unique<g2o::LinearSolverDense<g2o::BlockSolverX::PoseMatrixType>>();
// step 2. create block solver
std::unique_ptr<g2o::BlockSolverX> block_solver =
g2o::make_unique<g2o::BlockSolverX>(std::move(linear_solver));
// step 3. create optimization algorithm
g2o::OptimizationAlgorithm* algorithm
= new g2o::OptimizationAlgorithmLevenberg(std::move(block_solver));
// step 4. create optimizer
g2o::SparseOptimizer* optimizer = new g2o::SparseOptimizer;
optimizer->setAlgorithm(algorithm);
optimizer->setVerbose(true);	// to print optimization process

g2o를 사용하는데 있어서 가장 난해한 부분이다. Optimizer 객체 하나 생성하는데 뭐가 이렇게 복잡한 걸까. 참고로 이렇게 내부에서 사용하는 기능을 외부에서 추상 클래스로 주입받아 사용하는 것을 전략 패턴이라 한다. 잠시 전략 패턴을 설명해보겠다.

전략 패턴

class AlgoBase { virtual void func(int a) = 0; }
class AlgoAA: public AlgoBase { virtual void func(int a) { printf("printf %d", a); } }
class AlgoBB: public AlgoBase { virtual void func(int a) { cout << "cout " << a; } }
class Foo{
	AlgoBase* algo;
    setAlgo(AlgoBase* _algo) { algo = _algo; }
    doSomthing(int a) { algo->func(a); }
}
int main() {
    Foo* foo = new Foo;
    AlgoBase* aa = new AlgoAA;
    foo->setAlgo(aa);
    foo->doSomthing(3);	// -> print 3
    AlgoBase* bb = new AlgoBB;
    foo->setAlgo(bb);
    foo->doSomthing(3);	// -> cout 3    
}

Foo 클래스에서 사용하고자 하는 기능이 있고 이 기능을 구현하는 다양한 알고리즘이 있다. Foo는 상황에 따라서 알고리즘을 바꾸고 싶다. 근데 다양한 알고리즘을 Foo 안에서 관리하고 싶진 않다. 알고리즘 추가되면 Foo를 또 수정해야 하니까.
그래서 외부 클래스에 알고리즘을 구현하기로 했다. 그런데 외부에서도 한 클래스에 같은 기능을 하는 다양한 함수를 구현하는 건 바람직 하지 않다. 그래서 알고리즘의 입출력 형식을 AlgoBase라는 클래스에 가상함수로 선언해 놓고 이를 상속 받은 AlgoAA와 AlgoBB에서 다른 알고리즘을 구현한다.
위 예제에서 AlgoAA와 AlgoBB는 숫자 출력 기능을 각각 printf와 cout을 통해 다르게 구현하였다.
이제 Foo입장에서는 내부 클래스를 하나도 수정하지 않고 외부에서 어떤 클래스를 주입 받을지만 선택하면 된다.
AlgoAA와 AlgoBB 모두 AlgoBase의 자식 클래스이기 때문에 Foo는 둘 중 하나를 AlgoBase로 받아서 사용하면 된다.

따라서 예제의 g2o optmizer 생성 과정에는 저런 전략 패턴이 세 단계로 들어갔다고 보면 된다. 전략 패턴을 쓴다는 것은 예제에 쓰인 클래스들을 대체할만한 다른 옵션들이 존재한다는 것을 암시한다. 어떤 경우에 어떤 옵션을 써야하는지가 이 포스트의 핵심이다.

Option 1, 2: Select linear solver and block solver

std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linear_solver = 
g2o::make_unique<g2o::LinearSolverDense<g2o::BlockSolverX::PoseMatrixType>>();

std::unique_ptr<g2o::BlockSolverX> block_solver =
g2o::make_unique<g2o::BlockSolverX>(std::move(linear_solver));

첫 번째로 선택해야 할 옵션은 linear solver 이다. linear solver 라는 것은 Ax=b와 같은 행렬식을 풀어주는 알고리즘을 말한다. 예제에서는 LinearSolverDense가 쓰였는데 이것은 LinearSolver의 자식 클래스 이고 다른 자식(옵션)들도 존재한다.

LinearSolverDense: A의 성질과 상관없이 일반적으로 모든 경우에 사용될 수 있지만 속도는 느릴 수 있다.
LinearSolverCholmod: A가 symmetric 한 경우 Cholesky factorization을 이용하여 행렬식을 빠르게 풀 수 있다. SLAM이나 BA에서 이런 경우가 많다.
LinearSolverCSparse: A가 아주 큰데 matrix 안에 0이 아닌 숫자가 주로 diagonal에만 있는 경우 효과적이다. 역시 SLAM이나 BA에서 이런 경우가 많다.

두 번째로 선택해야 할 옵션은 block solver다. 행렬 식을 블록 단위로 풀어주는 것 같은데 정확한 목적은 모르겠다. 예제에서는 BlockSolver를 상속받은 BlockSolverX가 사용되었는데 자식 클래스들은 다음과 같다.

BlockSolverX: 일반적으로 블록의 크기에 상관없이 사용할 수 있다.
BlockSolver_6_3: 3D SLAM이나 BA를 할 때 선택한다. 여기서 6은 6-dof camera pose(SE3)를 의미하고 3은 point landmark의 3차원 좌표(xyz)를 의미한다. 결국 6차원 경로와 3차원 지도를 최적화 할 때 쓰인다.
BlockSolver_7_3: monocular BA를 할 때 선택한다. monocular BA에서는 pose에 scale 변수를 더해줘야 하기 때문에 7차원 pose(Sim3)가 된다. 3은 똑같이 point landmark를 의미한다.
BlockSolver_3_2: 2차원 SLAM을 할 때 선택한다. 3은 3-dof camera pose(x, y, theta) 를 의미하고 2는 point landmark의 2차원 좌표(xy)를 의미한다.

자신이 푸는 문제에 맞춰 LinearSolver와 BlockSolver를 선택하여 linear_solver와 block_solver 객체를 생성하면 된다.

Option 3: Select nonlinear optimization algorithm

g2o::OptimizationAlgorithm* algorithm
= new g2o::OptimizationAlgorithmLevenberg(std::move(block_solver));

g2o::SparseOptimizer* optimizer = new g2o::SparseOptimizer;
optimizer->setAlgorithm(algorithm);
optimizer->setVerbose(true);

g2o는 nonlinear optimization library이기 때문에 이제 nonlinear solver를 만들어야 한다. nonlinear optimization을 푸는 방법은 역시나 다크프로그래머님께서 잘 정리하셨다. 이론적인 내용은 링크를 들어가서 보고 여기서는 코드에 집중하겠다. 예제에서는 OptimizationAlgorithmLevenberg을 사용하였는데 이것은 g2o::OptimizationAlgorithm의 자식 클래스이고 다른 옵션들도 있다.

OptimizationAlgorithmGaussNewton: Gauss-Newton method 를 구현한 클래스다.
OptimizationAlgorithmLevenberg: Levenberg–Marquardt algorithm 을 구현한 것이고 가장 일반적으로 사용된다.
StructureOnlySolver 같은 다른 옵션도 있지만 위 두개만으로 충분한 것 같다.

원하는 알고리즘 객체를 생성하고 이를 optimizer->setAlgorithm(algorithm); 으로 주입해주면 optimizer 빌딩 과정이 끝난다. 이제 이 optimizer를 이용해서 간단한 문제를 풀어보자.

3.3 Construct a graph example

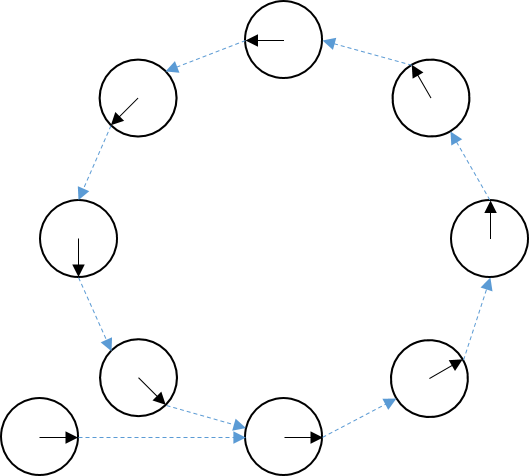
다음은 예제에서 만들 그래프를 그림으로 그린 것이다. 화살표가 달린 원은 vertex를 의미한다. (graph에서 node라는 용어 대신 vertex라는 용어도 흔히 쓰인다. g2o에서는 vertex로 표현하므로 여기서부터는 vertex 라는 용어로 통일하겠다.) 왼쪽 아래 첫 번째 vertex가 있고 이곳을 원점으로 하여 두 번째 vertex부터 원형으로 회전하여 다시 두 번째 vertex 자리로 돌아올 것이다. 각 vertex를 카메라 포즈로 생각하면 된다. 첫 두 개의 vertex는 pose를 주고 고정시켜 놓고 나머지 pose들은 기본 값을 주지 않고 pose 사이의 관계 정보를 가진 edge를 통해 optimizer로 계산할 것이다. example graph

3.3.1 Set fixed vertices

g2o에서는 6자유도를 가진 3차원 pose를 SE3Quat이라는 클래스로 표현한다. 3차원 pose를 (x, y, z, qx, qy, qz) 즉 3차원 좌표와 quaternion의 앞 3자리로 표현한다. qw는 나머지 세 개를 통해 구할 수 있기 때문에 생략한다.
SE3Quat는 Eigen::Quaterniond와 Eigen::Vector3d 변수로 초기화 할 수 있고 이를 addPoseVertex() 함수를 통해 optimizer에 추가된다.
함수 안에서 3차원 pose를 표현하는 g2o::SE3Quat& pose 정보를 이용하여 pose vertex 변수인 g2o::VertexSE3* v_se3의 초기값을 지정하고 optimizer->addVertex(v_se3);하여 optimizer에 vertex를 추가한다.
gt_poses는 추후 edge를 만들기 위해 모든 vertex pose를 저장하는 std::vector<g2o::SE3Quat> 이다.

int main()
{
	// ...
    Eigen::Vector3d tran;
    Eigen::Quaterniond quat;

    // first vertex at origin
    tran = Eigen::Vector3d(0,0,0);
    quat.setIdentity();
    g2o::SE3Quat pose0(quat, tran);
    addPoseVertex(optimizer, pose0, true);
    gt_poses.push_back(pose0);

    // second vertex at 1,0,0
    tran = Eigen::Vector3d(1,0,0);
    quat.setIdentity();
    g2o::SE3Quat pose1(quat, tran);
    addPoseVertex(optimizer, pose1, true);
    gt_poses.push_back(pose1);
    // ...
}

int getNewID()
{
    static int vertex_id = 0;
    return vertex_id++;
}

void addPoseVertex(g2o::SparseOptimizer* optimizer, g2o::SE3Quat& pose, bool set_fixed)
{
    g2o::VertexSE3* v_se3 = new g2o::VertexSE3;
    v_se3->setId(getNewID());
    if(set_fixed)
        v_se3->setEstimate(pose);
    v_se3->setFixed(set_fixed);
    optimizer->addVertex(v_se3);
}

3.3.2 Set variable vertices

첫 번째 vertex를 원점에 고정시켜놨고 나머지 vertex들은 최적화 대상이다. 이들을 원둘레를 따라 배치할 건데 원둘레를 따라 생기는 pose는 gt_poses에만 저장하고 vertex에는 입력하지 않는다.
(addPoseVertex(optimizer, abspose, false)에서 set_fixed에 false 입력하면 초기값을 넣지 않음)
이렇게 하면 graph에 vertex는 추가가 되지만 초기값이 모두 0인 상태다.

int main()
{
	// ...
    const double PI = 3.141592653589793;
    const int CIRCLE_NODES = 8;
    const double CIRCLE_RADIUS = 2;
    double angle = 2.*PI/double(CIRCLE_NODES);
    Eigen::Quaterniond quat;
    quat = Eigen::AngleAxisd(angle, Eigen::Vector3d(0,0,1));
    Eigen::Vector3d tran = Eigen::Vector3d(CIRCLE_RADIUS*sin(angle),
    CIRCLE_RADIUS - CIRCLE_RADIUS*cos(angle), 0.);
    // relative pose between consecutive pose along the circle
    g2o::SE3Quat relpose(quat, tran);

    for(int i=0; i<CIRCLE_NODES; i++)
    {
        g2o::SE3Quat abspose = gt_poses.back() * relpose;
        addPoseVertex(optimizer, abspose, false);
        gt_poses.push_back(abspose);
    }
    // ...
}

3.3.3 Set edges between vertices

vertex에 값이 없더라도 vertex 사이의 관계를 edge를 통해 정의해주면 최적화를 통해 vertex state를 복원할 수 있다. 다음은 pose 사이의 상대 pose를 계산하여 edge를 만들고 추가하는 코드다.
처음엔 for문에서 연속된 두 pose 사이의 관계를 입력하고 그 다음엔 loop closing을 만들기 위해 pose 1과 pose N-1 사이의 관계로 edge로 추가해주었다. addEdgePosePose는 edge를 추가하는 함수인데 내부에서 g2o::EdgeSE3 객체를 생성하며 optmizer에 추가한다.
g2o::EdgeSE3는 전역 pose (SE3Quat) 사이의 관계를 상대 pose (SE3Quat)로 측정한 값을 가진 객체이다. 이를 optimizer->addEdge(edge); 함수를 통해 추가하면 두 vertex 사이에 edge가 추가된다.

int main()
{
    // ...
    g2o::SE3Quat relpose;
    // add edge between poses
    for(size_t i=1; i<gt_poses.size(); i++)
    {
        // relpose: pose[i-1] w.r.t pose[i]
        relpose = gt_poses[i-1].inverse() * gt_poses[i];
        addEdgePosePose(optimizer, i-1, i, relpose);
    }

    // the last pose supposed to be the same as gt_poses[1]
    relpose = gt_poses[1].inverse() * gt_poses.back();
    addEdgePosePose(optimizer, 1, int(gt_poses.size()-1), relpose);
    // ...
}

void addEdgePosePose(g2o::SparseOptimizer* optimizer, int id0, int id1, g2o::SE3Quat& relpose)
{
    g2o::EdgeSE3* edge = new g2o::EdgeSE3;
    edge->setVertex(0, optimizer->vertices().find(id0)->second);
    edge->setVertex(1, optimizer->vertices().find(id1)->second);
    edge->setMeasurement(relpose);
    Eigen::MatrixXd info_matrix = Eigen::MatrixXd::Identity(6,6) * 10.;
    edge->setInformation(info_matrix);
    optimizer->addEdge(edge);
}

3.4 Optimize and write files

optimizer에 vertex와 edge를 추가했다면 그래프는 만들어진 것이다. 이제 vertex parameter를 최적화 하면 된다. 그리고 그 전후의 결과를 파일로 출력하여 비교해 보자.
최적화를 하기 전에 반드시 initializeOptimization() 함수를 실행해야 한다. g2o::SparseOptmizer 클래스에는 load(), save() 함수가 있는데 vertex와 edge 정보를 파일로 입출력할 수 있는 함수다. 여기서는 코드에서 그래프를 구성하기 때문에 save()를 통해 만들어진 그래프를 저장한다.
optimizer->optimize(100);를 실행하면 실제 최적화를 위한 연산을 한다. 입력으로 넣은 100은 최대 iteration 수다.

int main()
{
    // ...
    optimizer->initializeOptimization();

    std::string filename;
    filename = std::string(PRJ_PATH) + "/../igdata/before_opt.g2o";
    optimizer->save(filename.c_str());

    optimizer->optimize(100);

    filename = std::string(PRJ_PATH) + "/../igdata/after_opt.g2o";
    optimizer->save(filename.c_str());
    
    return 0;
}

3.5 Result

실행 결과는 다음과 같다. 실제 실행시에는 더 많은 정보가 뜨는데 줄이 넘어가서 일부만 붙였다. chi2는 에러를 나타내고 time은 수행 시간을 의미한다. 58번째 반복에서 에러가 0으로 수렴하여 자동종료 되었다.

output

iteration= 0	 chi2= 179.482061	 time= 0.000947222
iteration= 1	 chi2= 178.264733	 time= 0.00585554
iteration= 2	 chi2= 176.419299	 time= 0.00109663
iteration= 3	 chi2= 174.181579	 time= 0.00121086
...
iteration= 55	 chi2= 0.000000	 time= 0.000745319
iteration= 56	 chi2= 0.000000	 time= 0.0021958
iteration= 57	 chi2= 0.000000	 time= 0.000744429
iteration= 58	 chi2= 0.000000	 time= 0.00219608

다음은 최적화를 하기 전의 그래프 상태와 후의 그래프 상태를 텍스트로 출력한 것이다. 출력형식은 다음과 같다.

VERTEX_SE3:QUAT: SE3Quat을 출력한 것으로 [vertex_id, x, y, z, qx, qy, qz, qw] 이렇게 8개 숫자로 표현한다.
EDGE_SE3:QUAT: EdgeSE3를 출력한 것으로 [vertex0_id, vertex1_id, x, y, z, qx, qy, qz, qw, [upper triangle of information matrx]] 형식으로 표현된다. edge는 information matrix와 함께 출력되는데 pose가 6차원이므로 information matrix는 6x6 matrix이다. 그런데 36개의 숫자를 쓰기는 너무 양이 많고 어차피 information matrix는 symmetric 하기 때문에 upper triangle에 해당하는 21개의 숫자만 출력한다.

before_opt.g2o를 보면 2번부터 9번까지의 vertex가 모두 0으로 초기화 된 것을 볼 수 있다.

// before_opt.g2o
VERTEX_SE3:QUAT 0 0 0 0 0 0 0 1 
FIX 0
VERTEX_SE3:QUAT 1 1 0 0 0 0 0 1 
FIX 1
VERTEX_SE3:QUAT 2 0 0 0 0 0 0 1 
VERTEX_SE3:QUAT 3 0 0 0 0 0 0 1 
VERTEX_SE3:QUAT 4 0 0 0 0 0 0 1 
VERTEX_SE3:QUAT 5 0 0 0 0 0 0 1 
VERTEX_SE3:QUAT 6 0 0 0 0 0 0 1 
VERTEX_SE3:QUAT 7 0 0 0 0 0 0 1 
VERTEX_SE3:QUAT 8 0 0 0 0 0 0 1 
VERTEX_SE3:QUAT 9 0 0 0 0 0 0 1 
EDGE_SE3:QUAT 0 1 1 0 0 0 0 0 1 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 1 2 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 2 3 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 3 4 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 4 5 1.41421 0.585786 0 -0 -0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 5 6 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 6 7 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 7 8 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 8 9 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 1 9 2.22045e-16 -2.22045e-16 0 0 0 1.66533e-16 1 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 

최적화를 한 후인 after_opt.g2o를 0으로 초기화 되었던 vertex들에 값이 제대로 계산된 것을 확인할 수 있다.

VERTEX_SE3:QUAT 0 0 0 0 0 0 0 1 
FIX 0
VERTEX_SE3:QUAT 1 1 0 0 0 0 0 1 
FIX 1
VERTEX_SE3:QUAT 2 2.41421 0.585786 0 0 0 0.382683 0.92388 
VERTEX_SE3:QUAT 3 3 2 0 0 0 0.707107 0.707107 
VERTEX_SE3:QUAT 4 2.41421 3.41421 0 0 0 0.92388 0.382683 
VERTEX_SE3:QUAT 5 1 4 0 0 0 1 -1.04083e-16 
VERTEX_SE3:QUAT 6 -0.414214 3.41421 0 0 0 0.92388 -0.382683 
VERTEX_SE3:QUAT 7 -1 2 0 0 0 -0.707107 0.707107 
VERTEX_SE3:QUAT 8 -0.414214 0.585786 0 0 0 -0.382683 0.92388 
VERTEX_SE3:QUAT 9 1 -2.28571e-16 0 0 0 2.38865e-16 1 
EDGE_SE3:QUAT 0 1 1 0 0 0 0 0 1 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 1 2 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 2 3 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 3 4 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 4 5 1.41421 0.585786 0 -0 -0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 5 6 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 6 7 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 7 8 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 8 9 1.41421 0.585786 0 0 0 0.382683 0.92388 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 
EDGE_SE3:QUAT 1 9 2.22045e-16 -2.22045e-16 0 0 0 1.66533e-16 1 10 0 0 0 0 0 10 0 0 0 0 10 0 0 0 10 0 0 10 0 10 

이번 포스트에서는 optmizer의 다양한 옵션에 대해서 알아보고 예제에서는 단순히 SE3 pose로만 구성된 그래프를 최적화 해보았다. 다음 포스트에서는 g2o의 다양한 vertex, edge 타입에 대해서 알아보겠다.